BangBienthien
Author:
Bùi Minh Quang
Last Updated:
10년 전
License:
Creative Commons CC BY 4.0
Abstract:
Đây là Bảng biến thiên

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
Đây là Bảng biến thiên

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
\documentclass[12pt,a4paper,oneside]{report}
%======= Packages=======
\usepackage[utf8]{vietnam}
\usepackage{amsmath, amsthm, amssymb}
\usepackage{graphicx}
\usepackage{color}
\usepackage{exscale}
%\usepackage[notref,notcite] {showkeys}
\usepackage[mathscr]{eucal}
\usepackage{enumerate}
\usepackage{fancyhdr}
\usepackage[unicode]{hyperref}
\usepackage[top=35mm, bottom=30mm, left=35mm, right=20mm]{geometry}
\usepackage{tkz-tab}
\begin{document}
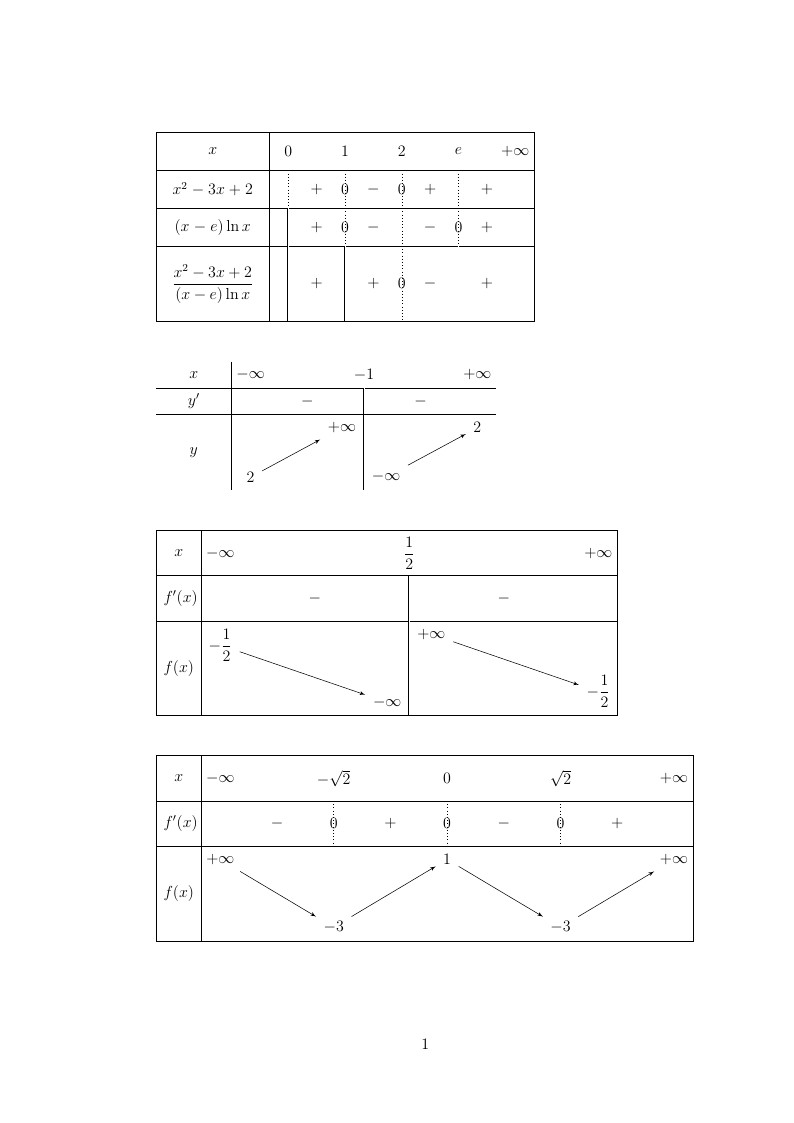
\begin{tikzpicture}
\tkzTabInit[lgt=3,espcl=1.5]%
{$x$ /1,
$x^2-3x+2$ /1,
$(x-e)\ln x$ /1,
$\dfrac{x^2-3x+2}{(x-e)\ln x}$ /2}
{$0$ , $1$ , $2$ , $e$ ,$+\infty$}
\tkzTabLine{ t,+,z,-,z,+,t,+,}
\tkzTabLine{ d,+,z,-,t,-,z,+,}
\tkzTabLine{ d,+,d,+,z,-,d,+,}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$x$ /.7, $y'$ /.7,$y$ /2}
{$-\infty$ ,$-1$ , $+\infty$}
\tkzTabLine{ ,-,d,-, }
\tkzTabVar{ - / $2$ ,+D- / $+\infty$/ $-\infty$ , + / $2$ }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=1.2,espcl=5]
{$x$ /1.2, $f’(x)$ /1.2,$f(x)$ /2.5}
{$-\infty$ , $\dfrac{1}{2}$ , $+\infty$}
\tkzTabLine{,-,d,-,}
\tkzTabVar{+/$-\dfrac{1}{2}$ ,-D+/$-\infty$/$+\infty$, -/$-\dfrac{1}{2}$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=1.2,espcl=3]
{$x$ /1.2, $f’(x)$ /1.2,$f(x)$ /2.5}
{$-\infty$ , $-\sqrt{2}$,$0$,$\sqrt{2}$, $+\infty$}
\tkzTabLine{,-,z,+,z,-,z,+,}
\tkzTabVar{+/$+\infty$ ,-/$-3$, +/$1$,-/$-3$,+/$+\infty$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[]
{$u$ /1.2, $f’(u)$ /1.2,$f(u)$ /2.5}
{,$-\dfrac{1}{4}$ , $\dfrac{-1+\sqrt{3}}{2}$ , $+\infty$,}
\tkzTabLine{t,h,d,+,z,-,d,h,t}
\tkzTabVar{LD/,-/$-\dfrac{5}{8}$ ,+/$\dfrac{2-\sqrt{3}}{2}$, -/$-\infty$,}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[lgt=3]%
{$t$/1,%
$f’(t)$ /1,%
$f(t)$ /2}%
{$-\infty$ , $-\frac{2}{3}$ , $\frac{1}{3}$ , $+\infty$}%
\tkzTabLine{ ,-, 0 ,+, 0 ,-, }
\tkzTabVar %
{
+/$0$,-/$-6$ ,+/$3$,-/$0$
}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$x$ /.7, $y'$ /.7,$y$ /2}
{$\frac 12$ ,$\frac 94$ , $4$}
\tkzTabLine{ d,+,0,-,d }
\tkzTabVar{ - / $\sqrt{14}$ ,+/$2\sqrt{7}$ , - / $\sqrt{14}$ }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]
{$t$/1,$f'(t)$/1,$f(t)$/2}
{$0$,$\frac12$,$+\infty$}
\tkzTabLine{,-,0,+,}
\tkzTabVar{+/$+\infty$,-/ $\frac34$/,+/$+\infty$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$ /1, $f(x)$ /2}
{$-\infty$ , $-\dfrac{2}{3}$ , $\dfrac{1}{3}$ , $+\infty$}
\tkzTabLine{ ,-, 0 ,+, 0 ,-, }
\tkzTabVar {+/$0$,-/$-6$ ,+/$3$,-/$0$}
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tikzset{h style/.style = {pattern=north west lines}}
\tkzTabInit[nocadre,lgt=2,espcl=3]
{$x$ /1, $f'(x)$ /1,$f(x)$ /2}
{$0$,$3$,$+\infty$}
\tkzTabLine{ d ,+ ,z,-, }
\tkzTabVar{D-/ $-\infty$ , +/ $ \frac{2}{9}$, -/ $0$ / }
\end{tikzpicture}
\vspace{1cm}
\begin{tikzpicture}
\tikzset{h style/.style = {pattern=north west lines}}
\tkzTabInit[nocadre,lgt=2,espcl=3]{$x$ /1, $f'(x)$ /1,$f(x)$ /2}{
$-\infty$,$-2$,$2$,$+\infty$}%
\tkzTabLine{ ,-, d ,h,d ,+, }
\tkzTabVar{+/ $1$ / , -DH/ $-3$ / , D-/ $-5$, +/ $1$ / }
\end{tikzpicture}
\vspace{1cm}
\begin{center}
\textbf{{\Large BANG BIEN THIEN CUA CAC HAM SO THUONG GAP O TRUONG THPT}}
\end{center}
\section{Hàm số bậc hai $\mathbf{y=ax^2+bx+c}$}
\subsection{ Trường hợp $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,-,}
\tkzTabVar{-/ $-\infty$,+/ $y_0$/,-/ $-\infty$}
\end{tikzpicture}
\subsection{ Trường hợp $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/1}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,+,}
\tkzTabVar{+/$+\infty$,-/ $y_0$/,+/$+\infty$}
\end{tikzpicture}
\section{Hàm số bậc ba $\mathbf{y=ax^3+bx^2+cx+d}$}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac <0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,-,}
\tkzTabVar{+/ $+\infty$,-/ $-\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac <0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$+\infty$}
\tkzTabLine{,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre,espcl=6]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$, $+\infty$}
\tkzTabLine{,+,}
\tkzTabVar{-/ $-\infty$,+/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac =0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,+,0,+,}
\tkzTabVar{-/ $-\infty$, R/,+/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac =0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_0$,$+\infty$}
\tkzTabLine{,-,0,-,}
\tkzTabVar{+/ $+\infty$, R/,-/ $-\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac >0}$ và $\mathbf{a>0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,+,0,-,0,+,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,+,0,-,0,+,}
\tkzTabVar{-/ $-\infty$, +/ $y_1$,-/ $y_2$, +/ $+\infty$ }
\end{tikzpicture}
\subsection{Trường hợp $\mathbf{\Delta=b^2-3ac >0}$ và $\mathbf{a<0}$}
\textbf{Bước 1:}Khởi tạo.\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\end{tikzpicture}\bigskip
\textbf{Bước 2: }Thêm dấu của đạo hàm:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,-,0,+,0,-,}
\end{tikzpicture}
\bigskip
\textbf{Bước 3: }Thêm chiều biến thiên:\bigskip
\begin{tikzpicture}
\tkzTabInit[nocadre]{$x$/1,$f'(x)$/1,$f(x)$/2}{$-\infty$,$x_1$,$x_2$,$+\infty$}
\tkzTabLine{,-,0,+,0,-,}
\tkzTabVar{+/ $+\infty$, -/$y_1$,+/ $y_2$, -/$-\infty$ }
\end{tikzpicture}
\end{document}